식스시그마의 핵심은 데이터가 평균을 중심으로 얼마나 퍼져 있는가(산포)를 관리하는 것입니다. 이를 가장 잘 보여주는 것이 바로 정규분포 곡선(종 모양 곡선)입니다.
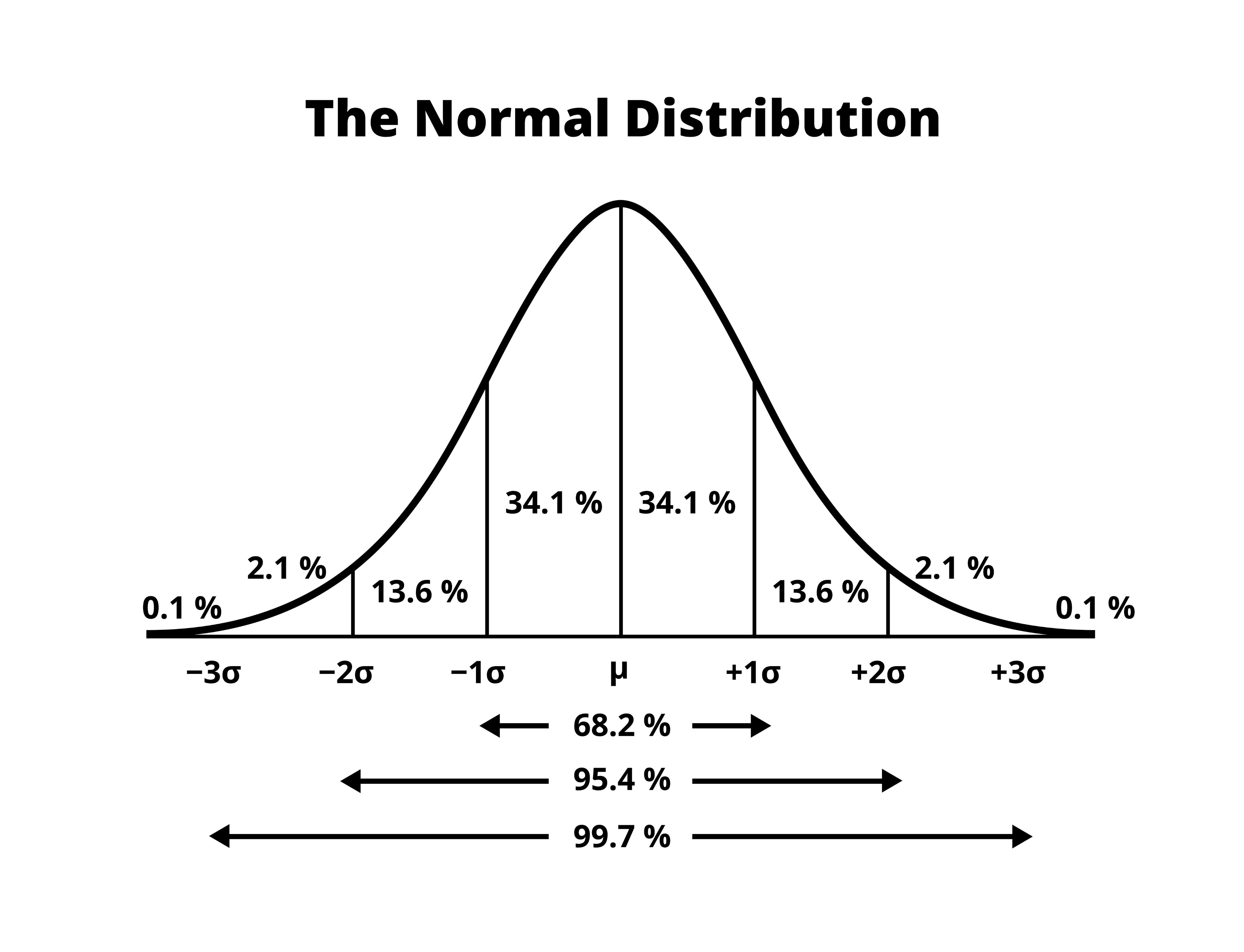
1. 정규분포와 시그마(σ)의 관계
정규분포에서 표준편차(σ)는 평균으로부터 떨어진 거리를 나타내는 단위입니다. 평균을 중심으로 좌우로 시그마만큼 이동할 때마다 그 안에 포함되는 데이터의 확률이 달라집니다.
- 1σ (68.27%): 데이터의 약 68%가 이 범위 안에 들어옵니다. (관리가 아주 느슨한 상태)
- 3σ (99.73%): 데이터의 99.7%가 범위 안에 들어옵니다. 일반적인 공정 관리의 기준입니다.
- 6σ (99.99966%): 데이터의 거의 100%가 범위 안에 들어옵니다. 불량률이 100만 개당 3.4개 수준으로 매우 정교한 상태입니다.
2. 식스시그마 계산법: Z-값 (Z-score)
식스시그마 수준을 계산할 때는 현재 공정의 결과물이 고객이 원하는 규격(Specification) 안에 얼마나 들어오는지를 측정합니다.
$$Z = \frac{\text{규격한계} - \text{평균}}{\sigma}$$
- LSL (Lower Spec Limit) : 하한 규격 (이보다 작으면 불량)
- USL (Upper Spec Limit) : 상한 규격 (이보다 크면 불량)
- 핵심 : 규격의 폭(USL - LSL) 안에 표준편차(σ)가 몇 번 들어가는지를 계산하는 것입니다. 그 횟수가 많을수록(예: 6번) 변동성이 작고 품질이 안정적이라는 뜻입니다.
3. 왜 '6' 시그마인가?
이론적으로 6σ는 규격 안에 표준편차가 6개 들어가는 매우 좁은 분포를 말합니다. 실제 산업 현장에서는 시간이 흐름에 따라 평균이 조금씩 이동(±1.5σ 이동)하는 것을 감안하더라도, 불량률을 극단적으로 낮게 유지하겠다는 의지가 담긴 숫자입니다.
요약하자면
- 시그마(σ)가 크다: 그래프가 옆으로 퍼짐 → 예측 불가능, 리스크 높음 (불량 많음)
- 시그마(σ)가 작다: 그래프가 가운데로 뾰족하게 모임 → 예측 가능, 안정적 (품질 우수)
